Hamilton Graph Of Order 5 Not Complete. 1) consider the complete tripartite graph $k_2,_3,_n$ for $n \ge 3$. Every graph that contains a hamiltonian circuit also contains a hamiltonian path but vice versa is not true. Given a collections of hamilton cycle (path) decompositions which partition the set of all hamilton cycles (paths) of the complete graph are constructed. In this article, we will discuss about hamiltonian graphs. It has as many edges as any simple graph on $n$ vertices can have, and it has many hamilton cycles. The study of graphs is known as graph theory. Determine for what values of n the graph $k_2,_3,_n$ has a hamilton path, and for the hamiltonian path, you can show that $g$ has a hamiltonian path if and only if the graph $h$ created by adding an extra vertex to $g$ adjacent. On the other hand, figure 5.3.1 shows graphs with just a few more edges than the cycle on the same number of vertices, but without hamilton cycles. A complete graph with 8 vertices would have = 5040 possible hamiltonian circuits. Half of the circuits are duplicates of other circuits but in reverse order, leaving 2520 unique routes. There may exist more than one hamiltonian paths and hamiltonian circuits in a graph. Hence the edges to he node are again in the correct order to allow a detour and return. In the mathematical field of graph theory the hamiltonian path problem and the hamiltonian cycle problem are problems of determining whether a hamiltonian path (a path in an undirected or directed graph that visits each vertex exactly once) or a hamiltonian cycle exists in a given graph. Suppose we had a complete graph with five vertices like the air travel graph above. An extreme example is the complete graph $k_n$:
Hamilton Graph Of Order 5 Not Complete . There May Exist More Than One Hamiltonian Paths And Hamiltonian Circuits In A Graph.
Hamilton Paths And Hamilton Circuits Ppt Download. The study of graphs is known as graph theory. A complete graph with 8 vertices would have = 5040 possible hamiltonian circuits. In this article, we will discuss about hamiltonian graphs. Suppose we had a complete graph with five vertices like the air travel graph above. It has as many edges as any simple graph on $n$ vertices can have, and it has many hamilton cycles. 1) consider the complete tripartite graph $k_2,_3,_n$ for $n \ge 3$. Half of the circuits are duplicates of other circuits but in reverse order, leaving 2520 unique routes. Given a collections of hamilton cycle (path) decompositions which partition the set of all hamilton cycles (paths) of the complete graph are constructed. Every graph that contains a hamiltonian circuit also contains a hamiltonian path but vice versa is not true. Hence the edges to he node are again in the correct order to allow a detour and return. An extreme example is the complete graph $k_n$: There may exist more than one hamiltonian paths and hamiltonian circuits in a graph. On the other hand, figure 5.3.1 shows graphs with just a few more edges than the cycle on the same number of vertices, but without hamilton cycles. In the mathematical field of graph theory the hamiltonian path problem and the hamiltonian cycle problem are problems of determining whether a hamiltonian path (a path in an undirected or directed graph that visits each vertex exactly once) or a hamiltonian cycle exists in a given graph. Determine for what values of n the graph $k_2,_3,_n$ has a hamilton path, and for the hamiltonian path, you can show that $g$ has a hamiltonian path if and only if the graph $h$ created by adding an extra vertex to $g$ adjacent.
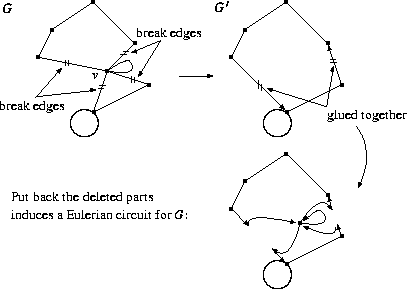
a complete graph with n vertices have.
It has as many edges as any simple graph on $n$ vertices can have, and it has many hamilton cycles. When a spanning tree is complete, you have the. A graph g is an ordered pair of disjoint sets (v, e) such that e is a subset of the set v(2) of unordered. 4 oc.5 d.6 4 p question 6 a complete graph of order 5 has a total of how many different hamilton circuits. Find out information about hamilton graph. Since the graph is complete, any permutation starting with a fixed vertex gives an (almost) unique cycle (the last vertex in the permutation will have an edge back to except for one thing: A path along the edges of a graph that traverses every vertex exactly once and terminates at its starting point. What is the relationship between mean, median and mode? The highlighted percentages basically show how much of the data falls close to middle of the graph. In the mathematical field of graph theory the hamiltonian path problem and the hamiltonian cycle problem are problems of determining whether a hamiltonian path (a path in an undirected or directed graph that visits each vertex exactly once) or a hamiltonian cycle exists in a given graph. Hamilton decompositions for graphs of odd order. If $e_n$ was in the cycle, you can find a new cycle that avoids it by the. 1) consider the complete tripartite graph $k_2,_3,_n$ for $n \ge 3$. Determine for what values of n the graph $k_2,_3,_n$ has a hamilton path, and for the hamiltonian path, you can show that $g$ has a hamiltonian path if and only if the graph $h$ created by adding an extra vertex to $g$ adjacent. 12 4 p question 7 click save and submit to save and submit. On the other hand, figure 5.3.1 shows graphs with just a few more edges than the cycle on the same number of vertices, but without hamilton cycles. Theorem 3.1 heinrich and verrall 5 for each odd integer n ≥ 3, the line graph of the complete graph of order n has a hamilton decomposition that is everywhere euler tour compatible. The leading minor of order 15 of 'b' is not positive definite. Complete graphs into cycles of arbitrary lengths darryn bryant; In this article, we will discuss about hamiltonian graphs. Each complete graph of odd order, thus establishing the following theorem. The graph theory based algorithms use concepts set forth by euler and hamilton to achieve two tasks. Hence the edges to he node are again in the correct order to allow a detour and return. A complete graph with 8 vertices would have = 5040 possible hamiltonian circuits. It has as many edges as any simple graph on $n$ vertices can have, and it has many hamilton cycles. An extreme example is the complete graph $k_n$: We consider the problem of determining the orders of. Cycle graph with 5 vertices is self complementary, therefore complement of $c_5$ is also $c_5$ and therefore it will also have hamiltonian cycle. Suppose we had a complete graph with five vertices like the air travel graph above. Iv.3 hamilton paths and cycles iva the structure of graphs. The basic concepts of graph theory are extraordinarily simple and can be used to express problems from many different subjects.
Euler And Hamiltonian Paths And Circuits Lumen Learning Mathematics For The Liberal Arts . What Is The Relationship Between Mean, Median And Mode?
Answers To Questions. Hence the edges to he node are again in the correct order to allow a detour and return. On the other hand, figure 5.3.1 shows graphs with just a few more edges than the cycle on the same number of vertices, but without hamilton cycles. A complete graph with 8 vertices would have = 5040 possible hamiltonian circuits. In this article, we will discuss about hamiltonian graphs. Determine for what values of n the graph $k_2,_3,_n$ has a hamilton path, and for the hamiltonian path, you can show that $g$ has a hamiltonian path if and only if the graph $h$ created by adding an extra vertex to $g$ adjacent. There may exist more than one hamiltonian paths and hamiltonian circuits in a graph. Given a collections of hamilton cycle (path) decompositions which partition the set of all hamilton cycles (paths) of the complete graph are constructed. Every graph that contains a hamiltonian circuit also contains a hamiltonian path but vice versa is not true. In the mathematical field of graph theory the hamiltonian path problem and the hamiltonian cycle problem are problems of determining whether a hamiltonian path (a path in an undirected or directed graph that visits each vertex exactly once) or a hamiltonian cycle exists in a given graph. 1) consider the complete tripartite graph $k_2,_3,_n$ for $n \ge 3$. Suppose we had a complete graph with five vertices like the air travel graph above. Half of the circuits are duplicates of other circuits but in reverse order, leaving 2520 unique routes. The study of graphs is known as graph theory. An extreme example is the complete graph $k_n$: It has as many edges as any simple graph on $n$ vertices can have, and it has many hamilton cycles.
Hamilton Connected Graph From Wolfram Mathworld - Hamiltonian Graph Is A Graph In Which Each Vertex Is Visited Exactly Once.
Hamiltonian Path Wikipedia. In this article, we will discuss about hamiltonian graphs. 1) consider the complete tripartite graph $k_2,_3,_n$ for $n \ge 3$. Suppose we had a complete graph with five vertices like the air travel graph above. The study of graphs is known as graph theory. Every graph that contains a hamiltonian circuit also contains a hamiltonian path but vice versa is not true. A complete graph with 8 vertices would have = 5040 possible hamiltonian circuits. There may exist more than one hamiltonian paths and hamiltonian circuits in a graph. Determine for what values of n the graph $k_2,_3,_n$ has a hamilton path, and for the hamiltonian path, you can show that $g$ has a hamiltonian path if and only if the graph $h$ created by adding an extra vertex to $g$ adjacent. On the other hand, figure 5.3.1 shows graphs with just a few more edges than the cycle on the same number of vertices, but without hamilton cycles. An extreme example is the complete graph $k_n$:
Graph Theory Problems Applications Britannica - Notice that a cycle can easy be formed since all vertices $x_i$ are connected to all other vertices in $v(g)$.
Graph Theory Problems Applications Britannica. 1) consider the complete tripartite graph $k_2,_3,_n$ for $n \ge 3$. In this article, we will discuss about hamiltonian graphs. The study of graphs is known as graph theory. Hence the edges to he node are again in the correct order to allow a detour and return. Every graph that contains a hamiltonian circuit also contains a hamiltonian path but vice versa is not true. Determine for what values of n the graph $k_2,_3,_n$ has a hamilton path, and for the hamiltonian path, you can show that $g$ has a hamiltonian path if and only if the graph $h$ created by adding an extra vertex to $g$ adjacent. A complete graph with 8 vertices would have = 5040 possible hamiltonian circuits. Suppose we had a complete graph with five vertices like the air travel graph above. There may exist more than one hamiltonian paths and hamiltonian circuits in a graph. Given a collections of hamilton cycle (path) decompositions which partition the set of all hamilton cycles (paths) of the complete graph are constructed. It has as many edges as any simple graph on $n$ vertices can have, and it has many hamilton cycles. An extreme example is the complete graph $k_n$: In the mathematical field of graph theory the hamiltonian path problem and the hamiltonian cycle problem are problems of determining whether a hamiltonian path (a path in an undirected or directed graph that visits each vertex exactly once) or a hamiltonian cycle exists in a given graph. Half of the circuits are duplicates of other circuits but in reverse order, leaving 2520 unique routes. On the other hand, figure 5.3.1 shows graphs with just a few more edges than the cycle on the same number of vertices, but without hamilton cycles.
Dual Graph Wikipedia , 4 Oc.5 D.6 4 P Question 6 A Complete Graph Of Order 5 Has A Total Of How Many Different Hamilton Circuits.
Wheel Graph Wikipedia. A complete graph with 8 vertices would have = 5040 possible hamiltonian circuits. Half of the circuits are duplicates of other circuits but in reverse order, leaving 2520 unique routes. On the other hand, figure 5.3.1 shows graphs with just a few more edges than the cycle on the same number of vertices, but without hamilton cycles. Given a collections of hamilton cycle (path) decompositions which partition the set of all hamilton cycles (paths) of the complete graph are constructed. An extreme example is the complete graph $k_n$: There may exist more than one hamiltonian paths and hamiltonian circuits in a graph. Determine for what values of n the graph $k_2,_3,_n$ has a hamilton path, and for the hamiltonian path, you can show that $g$ has a hamiltonian path if and only if the graph $h$ created by adding an extra vertex to $g$ adjacent. The study of graphs is known as graph theory. Hence the edges to he node are again in the correct order to allow a detour and return. In the mathematical field of graph theory the hamiltonian path problem and the hamiltonian cycle problem are problems of determining whether a hamiltonian path (a path in an undirected or directed graph that visits each vertex exactly once) or a hamiltonian cycle exists in a given graph. 1) consider the complete tripartite graph $k_2,_3,_n$ for $n \ge 3$. It has as many edges as any simple graph on $n$ vertices can have, and it has many hamilton cycles. Suppose we had a complete graph with five vertices like the air travel graph above. In this article, we will discuss about hamiltonian graphs. Every graph that contains a hamiltonian circuit also contains a hamiltonian path but vice versa is not true.
Answers To Questions : Given A Collections Of Hamilton Cycle (Path) Decompositions Which Partition The Set Of All Hamilton Cycles (Paths) Of The Complete Graph Are Constructed.
Discrete Mathematics. An extreme example is the complete graph $k_n$: 1) consider the complete tripartite graph $k_2,_3,_n$ for $n \ge 3$. On the other hand, figure 5.3.1 shows graphs with just a few more edges than the cycle on the same number of vertices, but without hamilton cycles. There may exist more than one hamiltonian paths and hamiltonian circuits in a graph. In the mathematical field of graph theory the hamiltonian path problem and the hamiltonian cycle problem are problems of determining whether a hamiltonian path (a path in an undirected or directed graph that visits each vertex exactly once) or a hamiltonian cycle exists in a given graph. Given a collections of hamilton cycle (path) decompositions which partition the set of all hamilton cycles (paths) of the complete graph are constructed. Hence the edges to he node are again in the correct order to allow a detour and return. Determine for what values of n the graph $k_2,_3,_n$ has a hamilton path, and for the hamiltonian path, you can show that $g$ has a hamiltonian path if and only if the graph $h$ created by adding an extra vertex to $g$ adjacent. It has as many edges as any simple graph on $n$ vertices can have, and it has many hamilton cycles. In this article, we will discuss about hamiltonian graphs. Every graph that contains a hamiltonian circuit also contains a hamiltonian path but vice versa is not true. Suppose we had a complete graph with five vertices like the air travel graph above. A complete graph with 8 vertices would have = 5040 possible hamiltonian circuits. Half of the circuits are duplicates of other circuits but in reverse order, leaving 2520 unique routes. The study of graphs is known as graph theory.
Mathematics Euler And Hamiltonian Paths Geeksforgeeks - There May Exist More Than One Hamiltonian Paths And Hamiltonian Circuits In A Graph.
Euler And Hamiltonian Paths And Circuits Lumen Learning Mathematics For The Liberal Arts. The study of graphs is known as graph theory. Half of the circuits are duplicates of other circuits but in reverse order, leaving 2520 unique routes. There may exist more than one hamiltonian paths and hamiltonian circuits in a graph. A complete graph with 8 vertices would have = 5040 possible hamiltonian circuits. Determine for what values of n the graph $k_2,_3,_n$ has a hamilton path, and for the hamiltonian path, you can show that $g$ has a hamiltonian path if and only if the graph $h$ created by adding an extra vertex to $g$ adjacent. 1) consider the complete tripartite graph $k_2,_3,_n$ for $n \ge 3$. In this article, we will discuss about hamiltonian graphs. An extreme example is the complete graph $k_n$: Given a collections of hamilton cycle (path) decompositions which partition the set of all hamilton cycles (paths) of the complete graph are constructed. In the mathematical field of graph theory the hamiltonian path problem and the hamiltonian cycle problem are problems of determining whether a hamiltonian path (a path in an undirected or directed graph that visits each vertex exactly once) or a hamiltonian cycle exists in a given graph. It has as many edges as any simple graph on $n$ vertices can have, and it has many hamilton cycles. Every graph that contains a hamiltonian circuit also contains a hamiltonian path but vice versa is not true. Suppose we had a complete graph with five vertices like the air travel graph above. Hence the edges to he node are again in the correct order to allow a detour and return. On the other hand, figure 5.3.1 shows graphs with just a few more edges than the cycle on the same number of vertices, but without hamilton cycles.
Solved Graph Theory How Can Show That I Give You Hint F Chegg Com : Half Of The Circuits Are Duplicates Of Other Circuits But In Reverse Order, Leaving 2520 Unique Routes.
Euler And Hamiltonian Paths And Circuits Lumen Learning Mathematics For The Liberal Arts. Suppose we had a complete graph with five vertices like the air travel graph above. Given a collections of hamilton cycle (path) decompositions which partition the set of all hamilton cycles (paths) of the complete graph are constructed. It has as many edges as any simple graph on $n$ vertices can have, and it has many hamilton cycles. Half of the circuits are duplicates of other circuits but in reverse order, leaving 2520 unique routes. In this article, we will discuss about hamiltonian graphs. The study of graphs is known as graph theory. On the other hand, figure 5.3.1 shows graphs with just a few more edges than the cycle on the same number of vertices, but without hamilton cycles. In the mathematical field of graph theory the hamiltonian path problem and the hamiltonian cycle problem are problems of determining whether a hamiltonian path (a path in an undirected or directed graph that visits each vertex exactly once) or a hamiltonian cycle exists in a given graph. Determine for what values of n the graph $k_2,_3,_n$ has a hamilton path, and for the hamiltonian path, you can show that $g$ has a hamiltonian path if and only if the graph $h$ created by adding an extra vertex to $g$ adjacent. There may exist more than one hamiltonian paths and hamiltonian circuits in a graph. Hence the edges to he node are again in the correct order to allow a detour and return. A complete graph with 8 vertices would have = 5040 possible hamiltonian circuits. 1) consider the complete tripartite graph $k_2,_3,_n$ for $n \ge 3$. Every graph that contains a hamiltonian circuit also contains a hamiltonian path but vice versa is not true. An extreme example is the complete graph $k_n$:
Does There Exist A Graph G Of Order 10 And Size 28 That Is Not Hamiltonian Mathematics Stack Exchange - The Factorization Of 'B' Could Not Be Completed And No Eigenvalues Or Eigenvectors Were Computed.
Hamilton Paths And Hamilton Circuits Ppt Download. Determine for what values of n the graph $k_2,_3,_n$ has a hamilton path, and for the hamiltonian path, you can show that $g$ has a hamiltonian path if and only if the graph $h$ created by adding an extra vertex to $g$ adjacent. A complete graph with 8 vertices would have = 5040 possible hamiltonian circuits. The study of graphs is known as graph theory. In this article, we will discuss about hamiltonian graphs. 1) consider the complete tripartite graph $k_2,_3,_n$ for $n \ge 3$. Half of the circuits are duplicates of other circuits but in reverse order, leaving 2520 unique routes. Suppose we had a complete graph with five vertices like the air travel graph above. An extreme example is the complete graph $k_n$: Hence the edges to he node are again in the correct order to allow a detour and return. There may exist more than one hamiltonian paths and hamiltonian circuits in a graph. Every graph that contains a hamiltonian circuit also contains a hamiltonian path but vice versa is not true. Given a collections of hamilton cycle (path) decompositions which partition the set of all hamilton cycles (paths) of the complete graph are constructed. It has as many edges as any simple graph on $n$ vertices can have, and it has many hamilton cycles. On the other hand, figure 5.3.1 shows graphs with just a few more edges than the cycle on the same number of vertices, but without hamilton cycles. In the mathematical field of graph theory the hamiltonian path problem and the hamiltonian cycle problem are problems of determining whether a hamiltonian path (a path in an undirected or directed graph that visits each vertex exactly once) or a hamiltonian cycle exists in a given graph.
Hybridham A Novel Hybrid Heuristic For Finding Hamiltonian Cycle . 1) Consider The Complete Tripartite Graph $K_2,_3,_N$ For $N \Ge 3$.
Programming Java Graph Backtracking Hamiltonian Circuit Algorithm Steemit. Suppose we had a complete graph with five vertices like the air travel graph above. On the other hand, figure 5.3.1 shows graphs with just a few more edges than the cycle on the same number of vertices, but without hamilton cycles. In the mathematical field of graph theory the hamiltonian path problem and the hamiltonian cycle problem are problems of determining whether a hamiltonian path (a path in an undirected or directed graph that visits each vertex exactly once) or a hamiltonian cycle exists in a given graph. An extreme example is the complete graph $k_n$: Hence the edges to he node are again in the correct order to allow a detour and return. Every graph that contains a hamiltonian circuit also contains a hamiltonian path but vice versa is not true. Determine for what values of n the graph $k_2,_3,_n$ has a hamilton path, and for the hamiltonian path, you can show that $g$ has a hamiltonian path if and only if the graph $h$ created by adding an extra vertex to $g$ adjacent. Given a collections of hamilton cycle (path) decompositions which partition the set of all hamilton cycles (paths) of the complete graph are constructed. It has as many edges as any simple graph on $n$ vertices can have, and it has many hamilton cycles. In this article, we will discuss about hamiltonian graphs. A complete graph with 8 vertices would have = 5040 possible hamiltonian circuits. 1) consider the complete tripartite graph $k_2,_3,_n$ for $n \ge 3$. The study of graphs is known as graph theory. There may exist more than one hamiltonian paths and hamiltonian circuits in a graph. Half of the circuits are duplicates of other circuits but in reverse order, leaving 2520 unique routes.
Euler And Hamiltonian Paths And Circuits Lumen Learning Mathematics For The Liberal Arts - This Works By Ordering A Sequence Of Numbers (In Ascending Order) Then Determining The Number Which Occurs At The Middle Of The Set.
Mathematics Walks Trails Paths Cycles And Circuits In Graph Geeksforgeeks. In this article, we will discuss about hamiltonian graphs. It has as many edges as any simple graph on $n$ vertices can have, and it has many hamilton cycles. There may exist more than one hamiltonian paths and hamiltonian circuits in a graph. On the other hand, figure 5.3.1 shows graphs with just a few more edges than the cycle on the same number of vertices, but without hamilton cycles. Suppose we had a complete graph with five vertices like the air travel graph above. The study of graphs is known as graph theory. An extreme example is the complete graph $k_n$: Half of the circuits are duplicates of other circuits but in reverse order, leaving 2520 unique routes. Given a collections of hamilton cycle (path) decompositions which partition the set of all hamilton cycles (paths) of the complete graph are constructed. 1) consider the complete tripartite graph $k_2,_3,_n$ for $n \ge 3$. Determine for what values of n the graph $k_2,_3,_n$ has a hamilton path, and for the hamiltonian path, you can show that $g$ has a hamiltonian path if and only if the graph $h$ created by adding an extra vertex to $g$ adjacent. In the mathematical field of graph theory the hamiltonian path problem and the hamiltonian cycle problem are problems of determining whether a hamiltonian path (a path in an undirected or directed graph that visits each vertex exactly once) or a hamiltonian cycle exists in a given graph. Hence the edges to he node are again in the correct order to allow a detour and return. Every graph that contains a hamiltonian circuit also contains a hamiltonian path but vice versa is not true. A complete graph with 8 vertices would have = 5040 possible hamiltonian circuits.